How Bias and Variance Affect Machine Vision Systems

July 1, 2025

SHARE ALSO

Bias and variance shape how machine vision systems perform in real-world scenarios. High bias often causes models to miss complex patterns, while high variance leads to inconsistent predictions.

Key metrics like accuracy, precision, F1-score, and mean squared error help measure these effects.
Techniques such as cross-validation, data augmentation, and model complexity adjustment address these challenges.

A well-balanced bias-variance tradeoff machine vision system delivers reliable results and adapts better to new data.

Key Takeaways

Bias causes models to miss important details, leading to underfitting and poor performance on all data.
Variance makes models sensitive to noise, causing overfitting and poor results on new images.
Balancing bias and variance helps machine vision systems make accurate and reliable predictions.
Techniques like cross-validation, data augmentation, and regularization reduce errors and improve model performance.
Learning curves and validation metrics help detect underfitting and overfitting early for better model tuning.

Bias and Variance

Bias in Vision Systems

Bias in machine vision systems refers to errors that come from the simplifying assumptions a model makes. When a model has high bias, it cannot capture the true patterns in the data. This often leads to underfitting, where the model performs poorly on both training and test images. Academic sources explain that bias is a component of reducible error. For example, a linear regression model may have high bias because it cannot learn complex shapes or textures in images. This makes it miss important details in tasks like object detection or image classification.

Tip: High bias can cause a vision system to overlook small but important features, such as cracks in a metal surface or subtle changes in a medical scan.

Researchers recommend using more flexible models or adding more features to reduce bias. Cross-validation helps check if a model is underfitting. Regularization and feature selection can also help balance the bias-variance tradeoff.

Variance in Vision Systems

Variance measures how much a model’s predictions change when trained on different sets of data. High variance means the model learns not only the true patterns but also the noise in the training images. This leads to overfitting, where the model does very well on training data but fails on new images. Decision trees and deep neural networks often show high variance, especially when they have many parameters.

Environmental factors can increase variance in machine vision systems. For example, changes in light, temperature, or dust can add noise to images and make the model less stable. The table below shows how different environmental factors impact variance and performance:

Environmental Factor	Impact on Variance and Performance	Example
Environmental Light	Adds noise, increases intensity	Use optical filters to reduce interference
Temperature	Increases sensor noise	Cooling systems help maintain camera performance
Dust	Degrades image clarity	Sealed enclosures prevent dust buildup
Humidity	Causes condensation, impairs imaging	Dehumidifiers keep lenses clear
Vibration	Blurs and distorts images	Vibration-dampening platforms stabilize cameras
Power Supply Voltage	Introduces noise, affects accuracy	Stable power supply reduces measurement errors
Electromagnetic Interference	Causes electronic noise in sensors	Circuit protection prevents interference

Machine vision researchers use several metrics to measure variance effects. The chart below shows SRCC values for different detection tasks, which help evaluate how much variance affects performance:

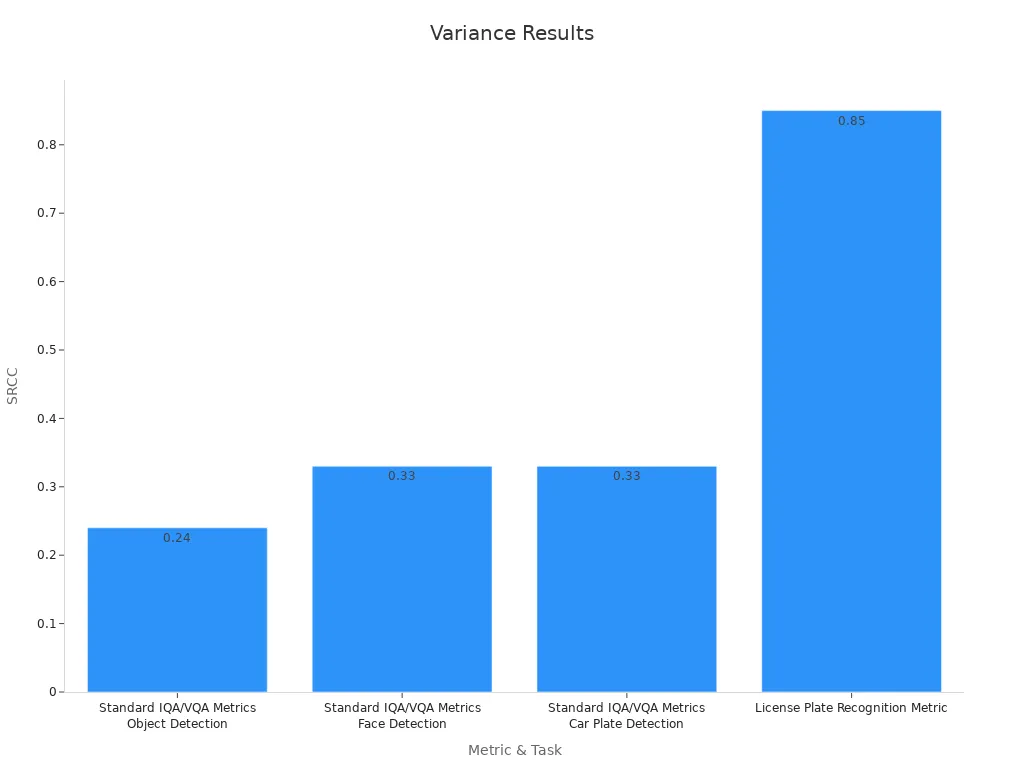
Common strategies to reduce variance include regularization, ensemble methods, and controlling model complexity. These methods help the model generalize better to new data and avoid overfitting.

Underfitting and Overfitting

High Bias: Underfitting

Underfitting happens when a model is too simple to capture the important patterns in data. This often results from high bias. The model cannot learn the true features, so it performs poorly on both training and new images. In image classification, underfitting can occur if a model uses only basic shapes or colors to identify objects. For example, a shallow decision tree may miss subtle differences between cats and dogs, leading to low accuracy.

A real-world case shows how underfitting appears in image classification. Researchers tested convolutional neural networks (CNNs) on the Yale Faces B dataset using only a 20×20 pixel background region. The model reached about 87.8% accuracy, much higher than random chance. This result suggests the model learned from irrelevant background features, not the actual faces. The table below summarizes these findings:

Dataset	Image Region Used	CNN Classification Accuracy	Random Chance Accuracy	Interpretation
Yale Faces B	20×20 pixel background	~87.8%	~3.57%	High accuracy on background shows bias and underfitting

Performance metrics such as low F1 score or low sensitivity can also signal high bias. These metrics help detect when a model fails to recognize important features in images.

Tip: Underfitting is like using a blurry lens. The model cannot see the details, so it misses key information.

High Variance: Overfitting

Overfitting occurs when a model is too complex and learns not only the true patterns but also the noise in the training data. This leads to high variance. The model performs very well on training images but fails on new, unseen data. In object detection, overfitting can happen if a model learns to associate dogs only with grassy backgrounds. When tested on images with different backgrounds, the model struggles to detect dogs.

A deep decision tree can memorize every detail in the training set, including random noise. This causes a large gap between training and validation accuracy. Learning curves often show low training error but high validation error, which signals overfitting. Researchers found that as model complexity increases, variance rises and accuracy on new data drops.

Overfitting signs include:
- High training accuracy but low test accuracy
- Large difference between training and validation errors
- Model performs well on familiar data but poorly on new data

To prevent overfitting, machine vision experts use regularization, data augmentation, and cross-validation. These methods help the model generalize better and avoid learning irrelevant details.

Overfitting is like memorizing answers for a test. The model does well on practice questions but cannot solve new problems.

Bias-Variance Tradeoff Machine Vision System

Bias-Variance Tradeoff

The bias-variance tradeoff machine vision system plays a central role in how well a predictive machine learning model performs. This tradeoff describes the balance between two types of errors: bias and variance. Bias measures how much a model’s predictions differ from the actual patterns in the data. Variance shows how much those predictions change when the model sees different training data. A good bias-variance tradeoff helps the system make accurate predictions on new images.

Researchers use several tools to diagnose and manage this tradeoff in machine vision.

Learning curves show how training and validation performance change as the model learns.
Validation metrics such as accuracy, precision, recall, and F1 score help measure both bias and variance.
Regularization controls model complexity and prevents overfitting.
Ensemble methods combine multiple models to reduce variance.
Hyperparameter tuning, including Bayesian optimization, helps find the best settings for the model.
Cross-validation gives a robust way to evaluate how well the model will perform on new data.

A bias-variance tradeoff machine vision system that balances these factors can adapt to new environments and deliver reliable results.

Theoretical studies explain the bias-variance tradeoff using statistical analyses. They show that balancing training and testing errors is key to avoiding overfitting. This approach helps machine vision systems generalize better, making them more useful in real-world tasks.

Model Complexity

Model complexity has a strong effect on the bias-variance tradeoff machine vision system. Simple models, like linear regression, often have high bias and low variance. They miss important details in images. Complex models, such as deep neural networks, can capture more patterns but may have high variance. They risk learning noise from the training data.

The total error in a machine vision system can be broken down into three parts:

Bias squared: The error from wrong assumptions in the model.
Variance: The error from sensitivity to small changes in the training data.
Irreducible error: The noise in the data that no model can remove.

This decomposition is written as:

Total Error = Bias² + Variance + Irreducible Error

This formula helps engineers understand where prediction errors come from and how to minimize them.

Comparative studies show how different models behave as complexity changes:

Model Type / Experiment	Model Complexity Change	Bias Behavior	Variance Behavior	Notes
k-NN Regression	Fewer neighbors (higher complexity)	Bias decreases	Variance increases	More complex models fit data better but may overfit
Linear Regression with Regularization	Stronger regularization (lower complexity)	Bias increases	Variance decreases	Simpler models generalize better but may underfit
Decision Trees, Polynomial Fitting	Deeper trees or higher degree	Bias decreases	Variance increases	Complex models capture more detail but risk overfitting
Neural Networks (Double Descent)	More layers or parameters	Bias decreases, then complex behavior	Variance rises, then falls	Error curve can dip twice as complexity grows

These results show that increasing model complexity usually lowers bias but raises variance. However, some modern models, like deep neural networks, can show more complex patterns, such as the double descent phenomenon.

Comparative analyses also reveal that the choice of error metric affects model selection. Absolute error and squared error penalize bias and variance differently. Absolute error may favor complex models with lower bias, while squared error prefers simpler models with lower variance. This insight helps engineers choose the right metric for their machine vision task.

A well-designed bias-variance tradeoff machine vision system aims to minimize total error. Engineers adjust model complexity, use regularization, and select proper evaluation metrics to achieve the best balance. This approach leads to robust and accurate machine vision systems that work well in real-world conditions.

Diagnosing and Balancing

Learning Curves

Learning curves help engineers understand how well a machine vision model learns from data. These curves plot training and validation scores as the size of the training set increases. When both training and validation errors stay high, the model shows underfitting, which means high bias. If the training error is low but the validation error is much higher, the model overfits, showing high variance. Researchers use learning curves to spot these problems early and adjust the model before deployment.

Academic studies have shown that learning curves can reveal trends in bias and variance during different learning phases. For example, in the early phase, models often show high variance, but as training continues, the variance usually drops. Tools like scikit-learn make it easy to generate and interpret these curves. Validation curves, which plot error against model complexity, also help find the right balance between underfitting and overfitting.

Engineers often use cross-validation and bootstrap sampling with learning curves to check if a model will perform well on new data.

Learning curves plot errors to diagnose bias and variance.
Underfitting appears as high errors on both curves.
Overfitting shows a large gap between training and validation errors.
Validation curves help choose the best model complexity.

Reducing Error

To build robust machine vision systems, engineers use several proven techniques to reduce error and balance bias and variance. Regularization methods, such as L2 regularization and dropout, help prevent overfitting by making the model less sensitive to noise. Data augmentation, like random cropping or noise injection, increases the variety of training images, which improves generalization.

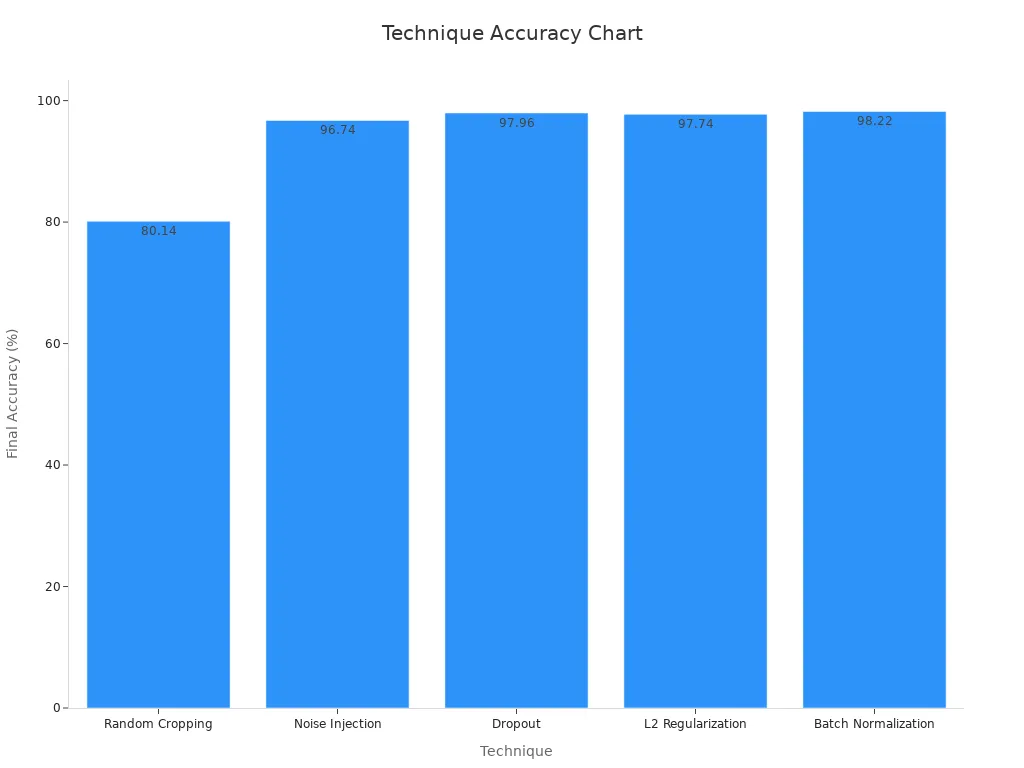
A table below shows how these techniques improve accuracy and stability:

Technique	Improvement Metric / Result
Random Cropping	Accuracy increased from 72.88% to 80.14%; Kappa from 0.43 to 0.57
Noise Injection	Accuracy improved from 44.0% to 96.74%
Dropout	Test accuracy improved from 0.9787 to 0.9796; Test loss reduced from 0.1086 to 0.0730
L2 Regularization	Test accuracy at 0.9774; Test loss at 0.1226
Batch Normalization	Test accuracy at 0.9822; Test loss at 0.0882

Case studies in healthcare and industry confirm that combining data augmentation with regularization leads to better accuracy and more reliable predictions. Automated machine learning tools now use these strategies to help models adapt to new environments and reduce errors caused by bias or variance.

Using a mix of diagnostic tools and error-reducing techniques helps machine vision systems stay accurate and reliable in real-world tasks.

Machine vision systems achieve better accuracy and reliability when engineers balance bias and variance. Techniques like cross-validation, regularization, and data augmentation help models generalize to new data.

Recent experiments show that these strategies improve accuracy and reduce errors in real-world tasks.

Industrial deployments use:
- Model selection and tuning
- Ensemble methods
- Continuous monitoring

For deeper learning, researchers explore advanced bias detection, diverse datasets, and explainable AI. Ongoing collaboration and transparent practices will support fair and robust machine vision in the future.

FAQ

What is the main difference between bias and variance in machine vision?

Bias means the model makes simple assumptions and misses important details. Variance means the model reacts too much to small changes in the data. Both can hurt accuracy in machine vision tasks.

How can someone tell if a vision model is underfitting or overfitting?

Underfitting shows high errors on both training and test data. Overfitting shows low training error but high test error. Learning curves help spot these problems early.

Why does model complexity matter in machine vision systems?

A simple model may miss patterns and underfit. A complex model may learn noise and overfit. Engineers adjust complexity to find the best balance for accurate results.

What are some easy ways to reduce overfitting in image classification?

Use data augmentation, like flipping or rotating images.
Add regularization, such as dropout or L2.
Try ensemble methods to combine different models.

Can bias and variance be removed completely from a machine vision system?

No model can remove all bias and variance. Some error always remains because of noise in the data. Engineers work to minimize these errors for better performance.